树状数组

       一个数组很大的时候，几项求和（不一定求和，求和最常见），累加就显得太耗时了，时间复杂度为O(n)，并且采用累加的方法还有一个局限，那就是，当修改掉数组中的元素后，仍然要你求数组中某段元素的和，就显得麻烦了。所以我们就要用到树状数组，时间复杂度为O（lgn），相比之下就快得多

         树状数组图：

        

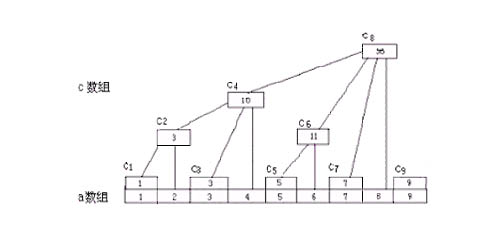
c1=a1，c2=a1+a2，c3=a3，c4=a1+a2+a3+a4，c5=a5，c6=a5+a6，c7=a7，c8=a1+a2+a3+a4+a5+a6+a7+a8，c9=a9，c10=a9+a10，c11=a11........c16=a1+a2+a3+a4+a5+.......+a16。

      分析上面的几组式子可知：

1. 当 i 为奇数时，ci=ai ；
2. 当 i 为偶数时，就要看 i 的因子中最多有二的多少次幂，例如，6 的因子中有 2 的一次幂，等于 2 ，所以 c6=a5+a6（由六向前数两个数的和），4 的因子中有 2 的两次幂，等于 4 ，所以 c4=a1+a2+a3+a4（由四向前数四个数的和）。

        有公式：cn =  a(n-2^k+1)+.........+an（其中 k 为 n 的二进制表示中从右往左数的 0 的个数，2^k则是n的因子中最大的2的次幂）。

         那么，如何求 2^k 呢？求法如下：

int lowbit(int i)
{  // 返回i的因子中含有 2的最大幂,如6的因子中最大2的幂是2^1 = 2 ，8的因子最大2次幂 2^3 = 8；
	return i&(-i);
}

lowbit（）的返回值就是 2^k 次方的值。

 

（一）创建树状数组

for(i=1;i<=n;i++)
	{
		scanf("%d",&e);
		a[i] = e;
		if(i&1)//奇数,树状数组与原始位置数据一样
			Tree_a[i] = a[i];
		else //偶数，树状数组对应位置存的为几项的和
		{
			int sum = 0;
			for(j=i+1-lowbit(i);j<=i;j++)	sum += a[j];//求出从a[i]与前 lowbit(i) 项的和
			Tree_a[i] = sum;
		}
	}//建好树状数组Tree_a[] ,  原始数组a[]

（二）当数组中的元素有变更时，树状数组就发挥它的优势了，算法如下（修改为给某个节点x加上 y，数组长度n ）：

        

void change(int x, int y,int n)
{//给x位置增加y，则x到n之间需要调整
	while(x<=n)
	{
		Tree_a[x] += y;
		x += lowbit(x);//只调整个别的
	}
}

（三）求x到y之间的数据的和（根据数组数组求）

SUM = f_sum(y) - f_sum(x-1);

int f_sum(int x)
{//返回前x个数的和
	if(x==0) return 0;
	int sum = 0;
	while( x>0 )
	{
		sum += Tree_a[x]; //求前x数的和
		x -= lowbit(x);
	}
	return sum;
}